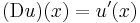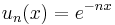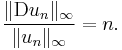Densely defined operator
In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere". Densely defined operators often arise in functional analysis as operations that one would like to apply to a larger class of objects than those for which they a priori "make sense".
Definition
A linear operator T from one topological vector space, X, to another one, Y, is said to be densely defined if the domain of T is a dense subset of X and the range of T is contained within Y.
Examples
- Consider the space C0([0, 1]; R) of all real-valued, continuous functions defined on the unit interval; let C1([0, 1]; R) denote the subspace consisting of all continuously differentiable functions. Equip C0([0, 1]; R) with the supremum norm ||·||∞; this makes C0([0, 1]; R) into a real Banach space. The differentiation operator D given by
- is a densely-defined operator from C0([0, 1]; R) to itself, defined on the dense subspace C1([0, 1]; R). Note also that the operator D is an example of an unbounded linear operator, since
- has
- This unboundedness causes problems if one wishes to somehow continuously extend the differentiation operator D to the whole of C0([0, 1]; R).
- The Paley–Wiener integral, on the other hand, is an example of a continuous extension of a densely-defined operator. In any abstract Wiener space i : H → E with adjoint j = i∗ : E∗ → H, there is a natural continuous linear operator (in fact it is the inclusion, and is an isometry) from j(E∗) to L2(E, γ; R), under which j(f) ∈ j(E∗) ⊆ H goes to the equivalence class [f] of f in L2(E, γ; R). It is not hard to show that j(E∗) is dense in H. Since the above inclusion is continuous, there is a unique continuous linear extension I : H → L2(E, γ; R) of the inclusion j(E∗) → L2(E, γ; R) to the whole of H. This extension is the Paley–Wiener map.